A CFrame, short for Coordinate Frame, is a data type used to rotate and position 3D objects. As either an object property or a standalone unit, a CFrame contains global x-, y-, and z-coordinates as well as rotation data for each axis. In addition, CFrames contain helpful functions for working with objects in the 3D space.
Some examples of CFrame applications in a game might be:
- Finding a far-off target point for a projectile, like the position of an enemy targeted by a player's laser blaster.
- Moving the camera so that it focuses on specific NPCs as a player interacts with them.
- Placing a status indicator directly above a player's head to show if they are paralyzed, boosted, poisoned, etc.
CFrame Basics
Positioning a CFrame
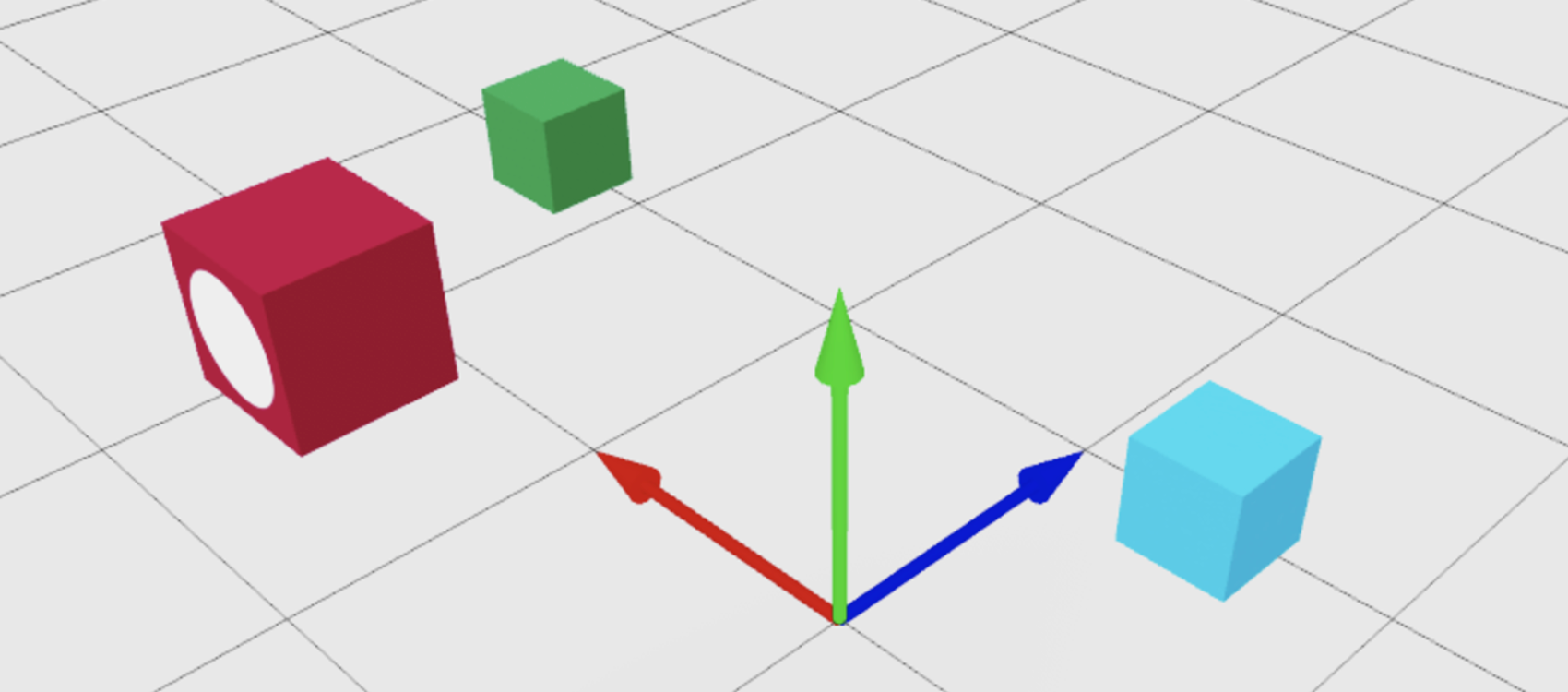
You can create an empty CFrame at the default position of (0, 0, 0) by using CFrame.new(). To position a CFrame at a specific point, provide x-, y-, and z-coordinates as arguments to CFrame.new(). In the following example, the redBlock part's CFrame property changes to newCFrame, repositioning it to (-2, 2, 4).
Alternatively, you can provide a new Vector3 position to CFrame.new() and achieve the same result:
Rotating a CFrame
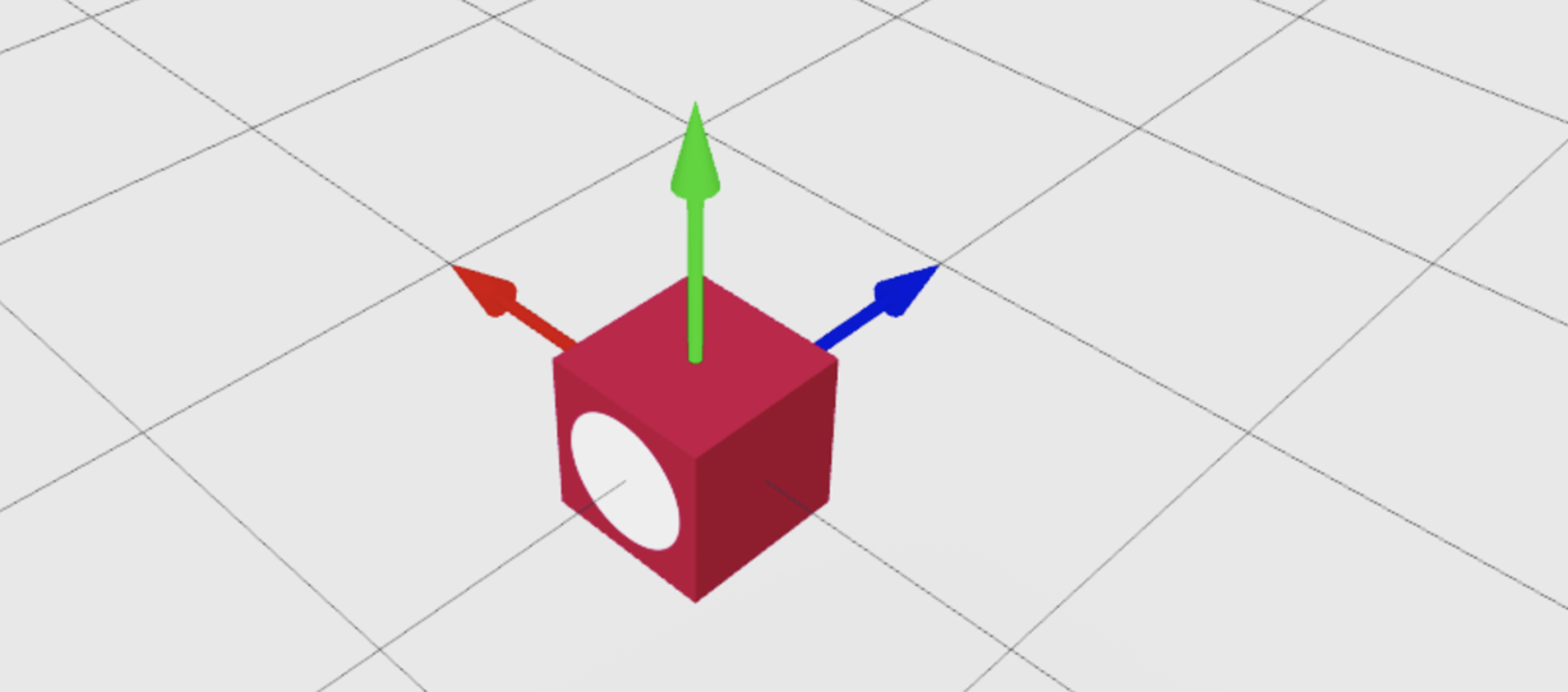
To create a rotated CFrame, use the CFrame.Angles() constructor, providing a rotation angle in radians for the desired axes. The parameters to CFrame.Angles() is in radians, not degrees. If you prefer degrees, use math.rad() to convert degrees to radians. In the following example, the redBlock part rotates 45 degrees counterclockwise on its y-axis.
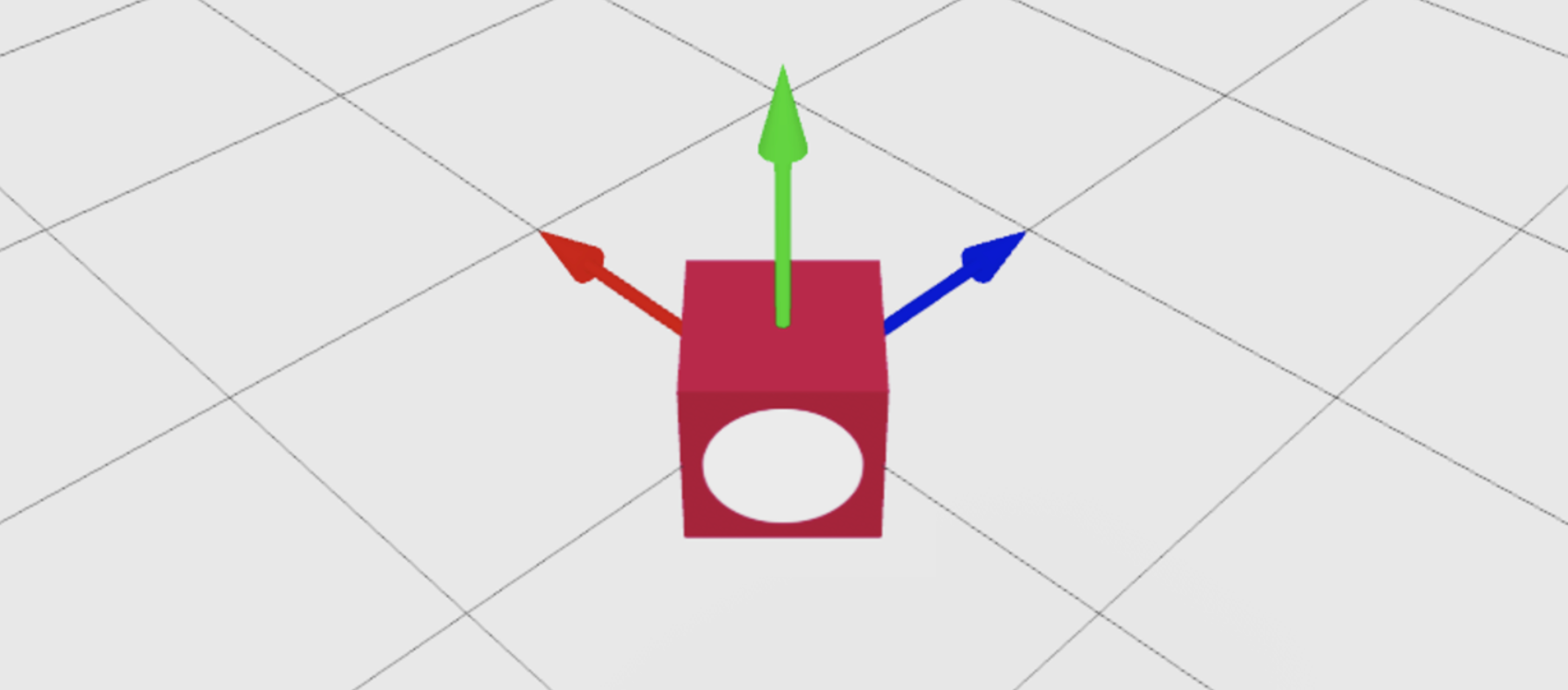
Facing Toward a Point
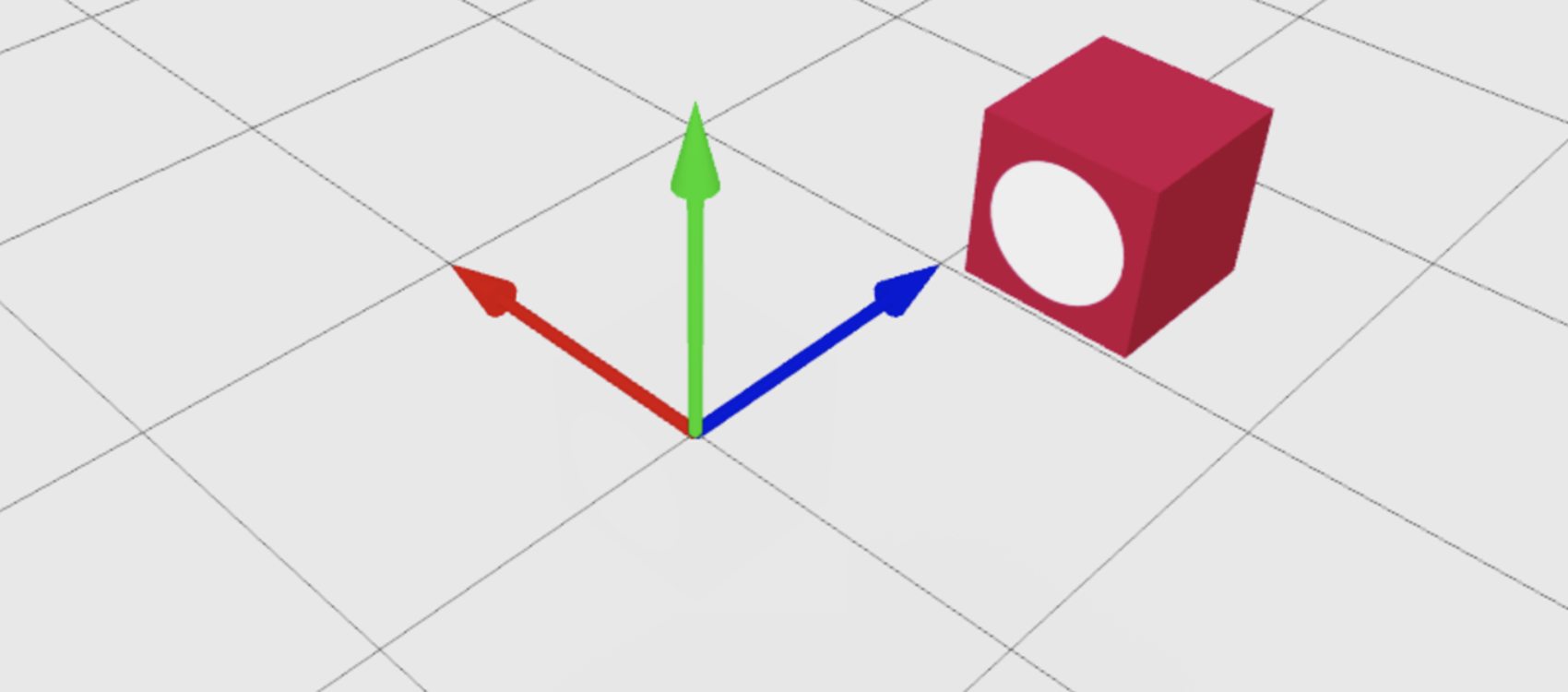
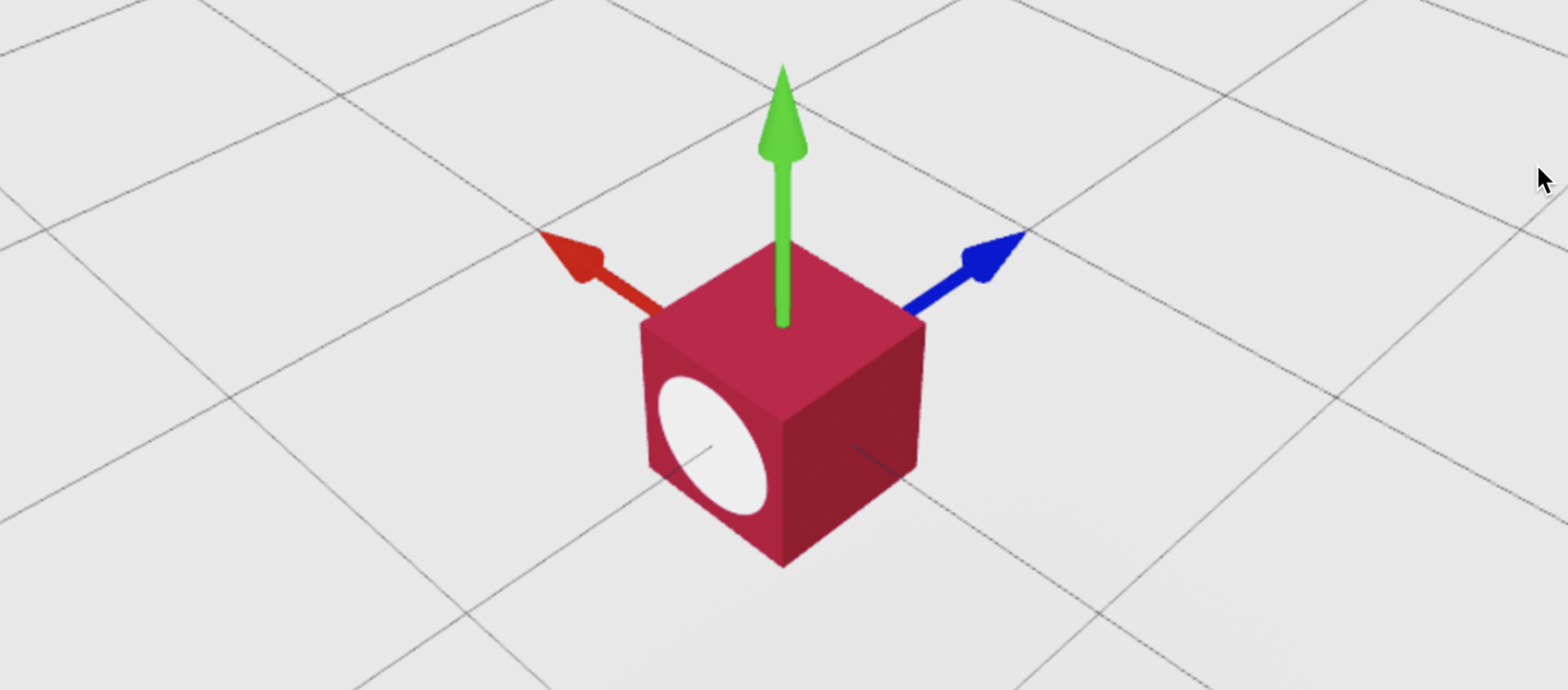
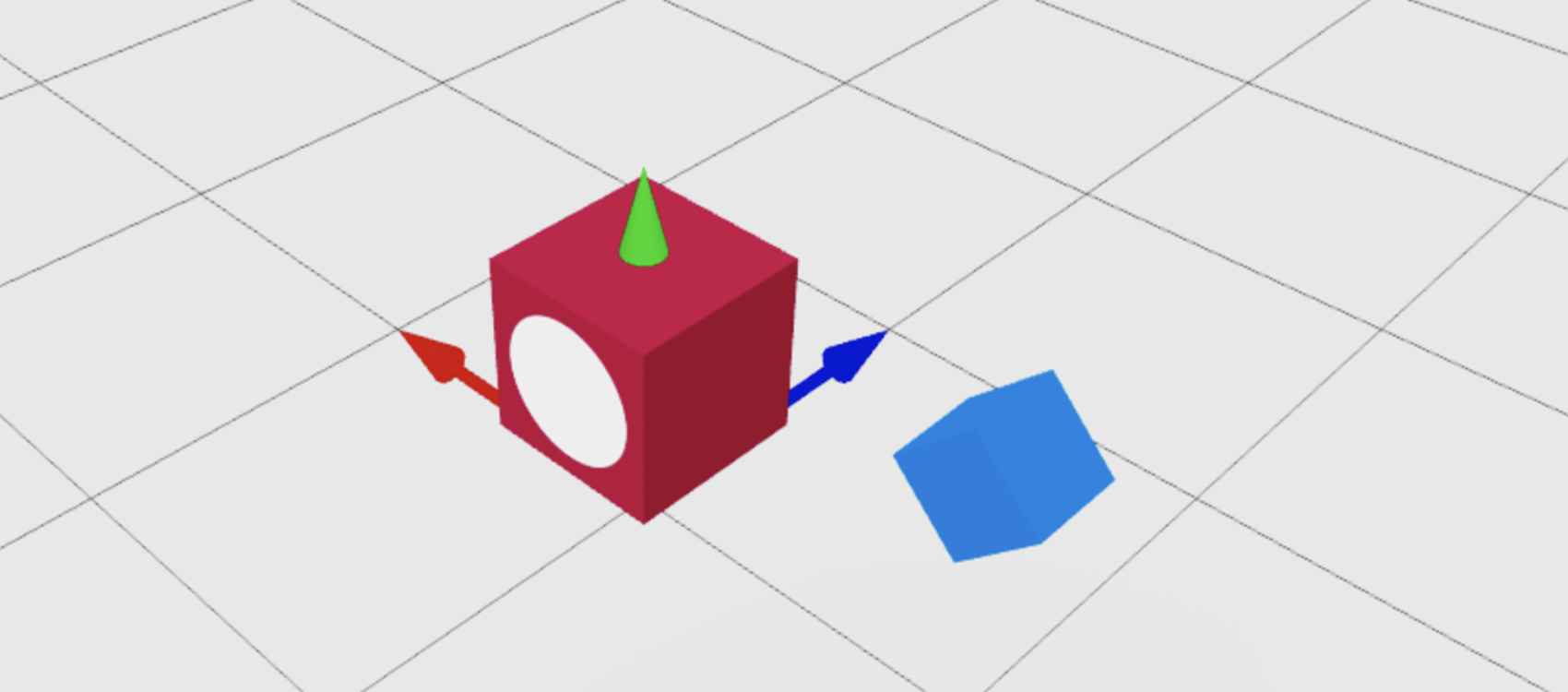
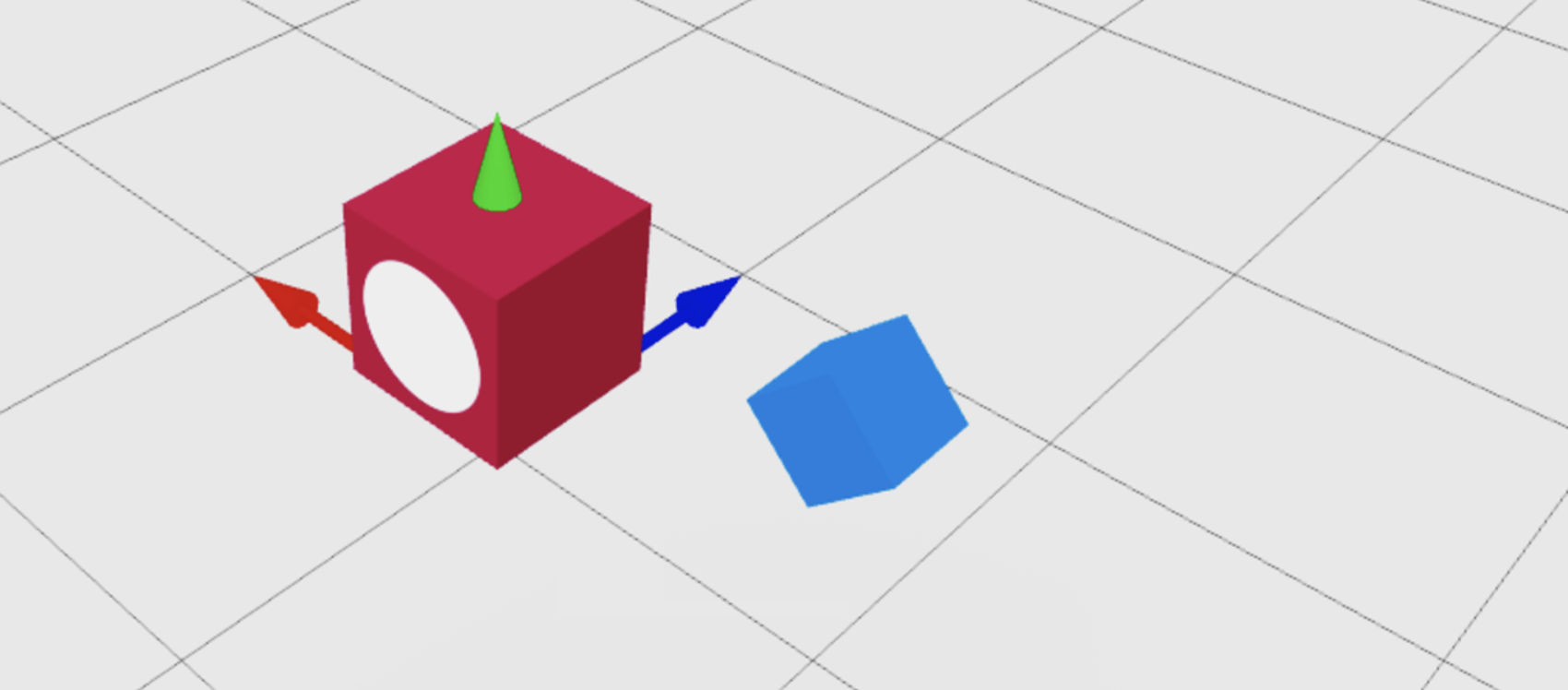
You can use CFrame.new() to point the front surface of a CFrame at a specific point in the world. In the following example, redBlock part positions at (0, 3, 0) and points its front surface, marked by the white circle, at the blueCube part.

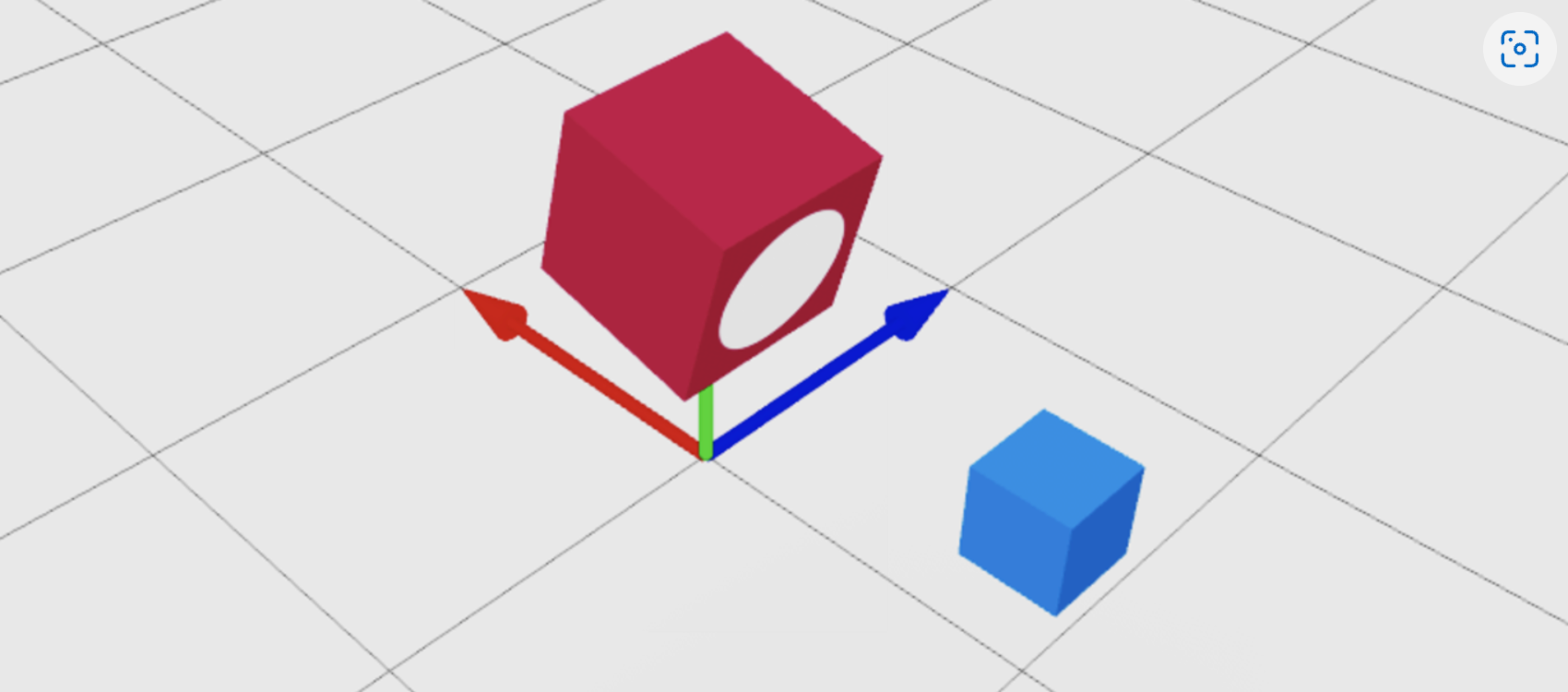
Offsetting a CFrame
To offset an object by a specific number of studs from its current position, add or subtract a Vector3 to or from a new CFrame at the object's position. To get a properly-formatted Vector3 position of an object to use with CFrame.new(), as seen here, its Position property (redBlock.Position) is a convenient shortcut.
You can use the same technique to offset an object from the position of another object. In the following example, a Vector3 adds to a new CFrame created at the blue cube's position instead of the block's position.
Dynamic CFrame Orientation
The CFrame.new() and CFrame.Angles() constructors reposition or rotate an object at a specific orientation within the world, but you sometimes can't rely on a fixed world position and rotation angle. For example:
- Placing a floating treasure directly in front of a player who may be standing anywhere in the world, facing any direction.
- Making a magical genie appear directly above a player's right shoulder.
In these cases, use CFrame methods instead of their constructors.
Relative Position
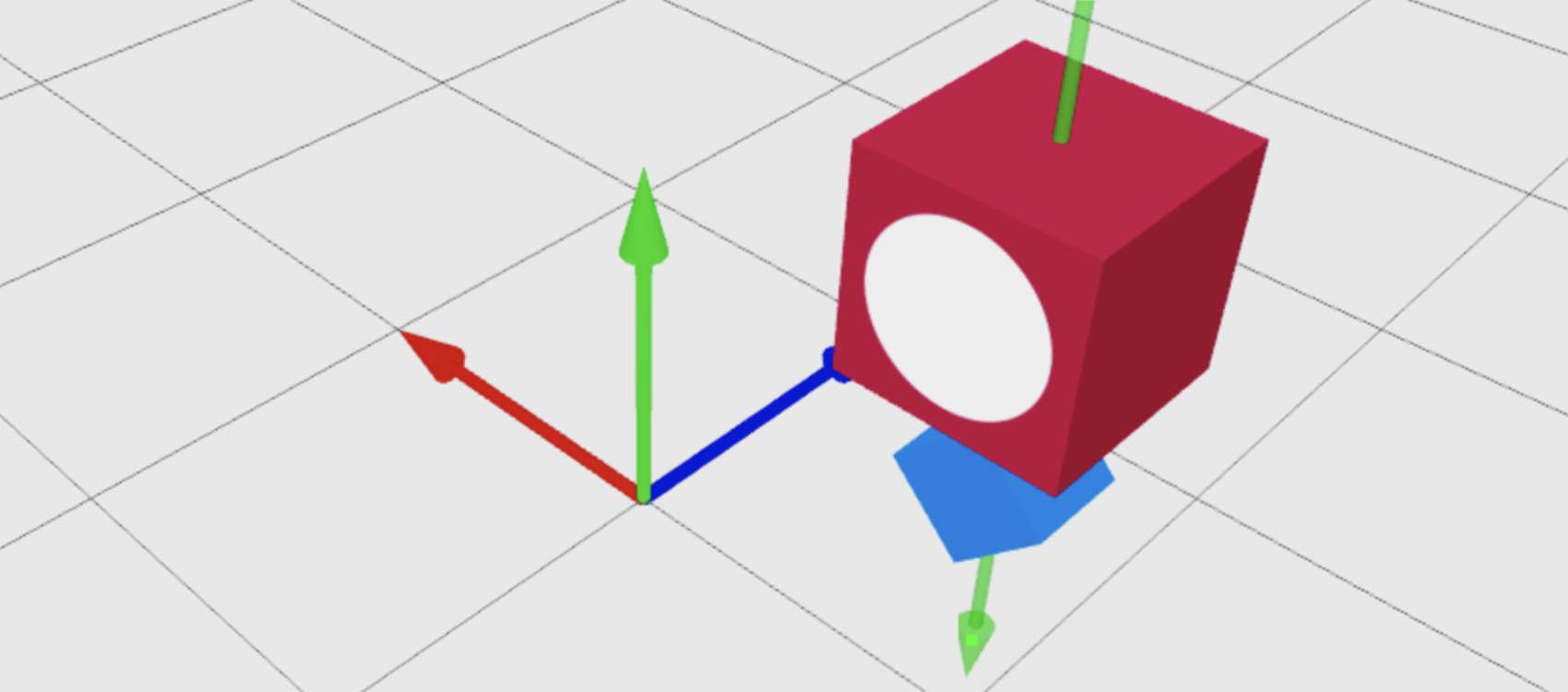
The CFrame:ToWorldSpace() function transforms an object's CFrame — respecting its own local orientation — to a new world orientation. This makes it ideal for offsetting a part relative to itself or another object, regardless of how it's currently positioned/rotated.
In the following example, the redBlock part offsets 2 studs relative to the y-axis of the blue cube (the green arrow pointing through it) and not relative to the global y-axis pointing straight up.
Relative Rotation
You can also use CFrame:ToWorldSpace() to rotate an object relative to itself. In the following example, the redBlock part rotates 70 degrees counterclockwise on its y-axis and 20 degrees clockwise on its z-axis.


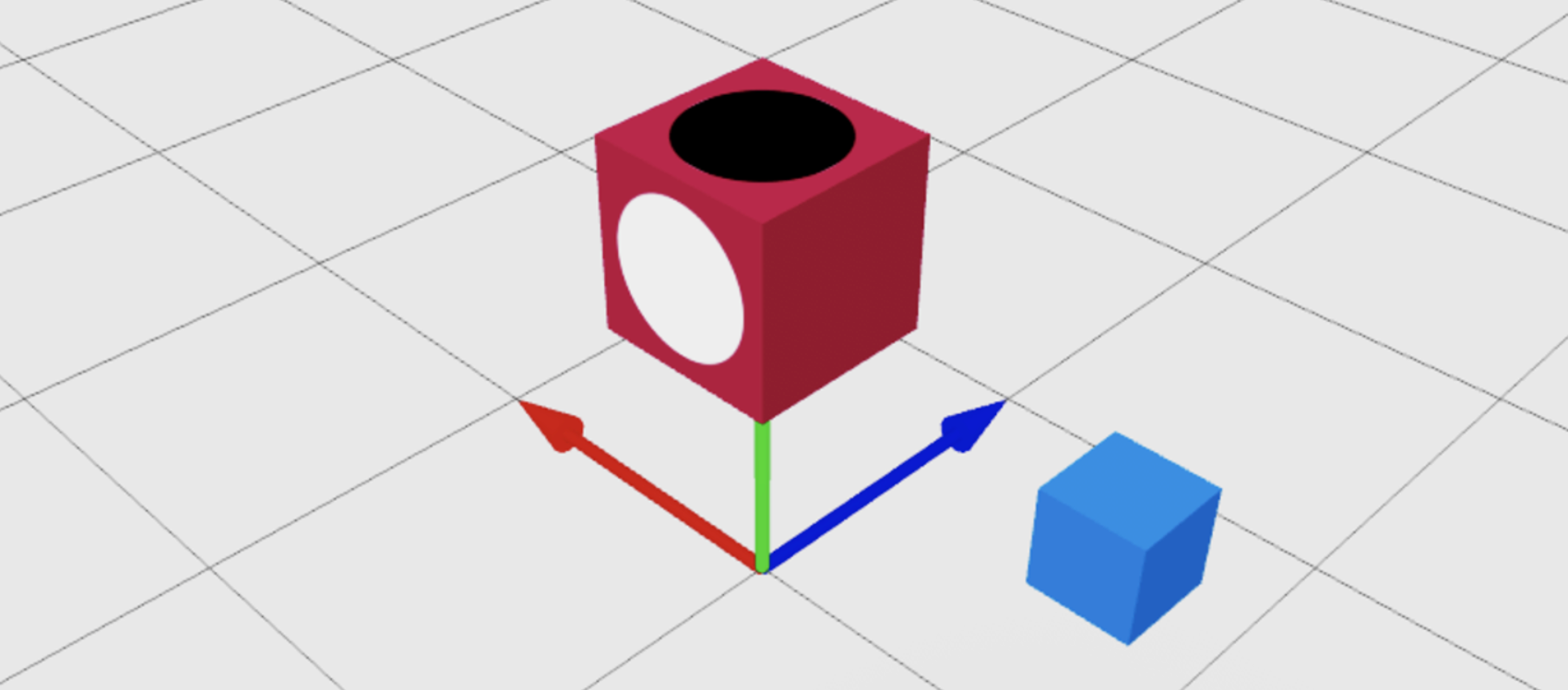
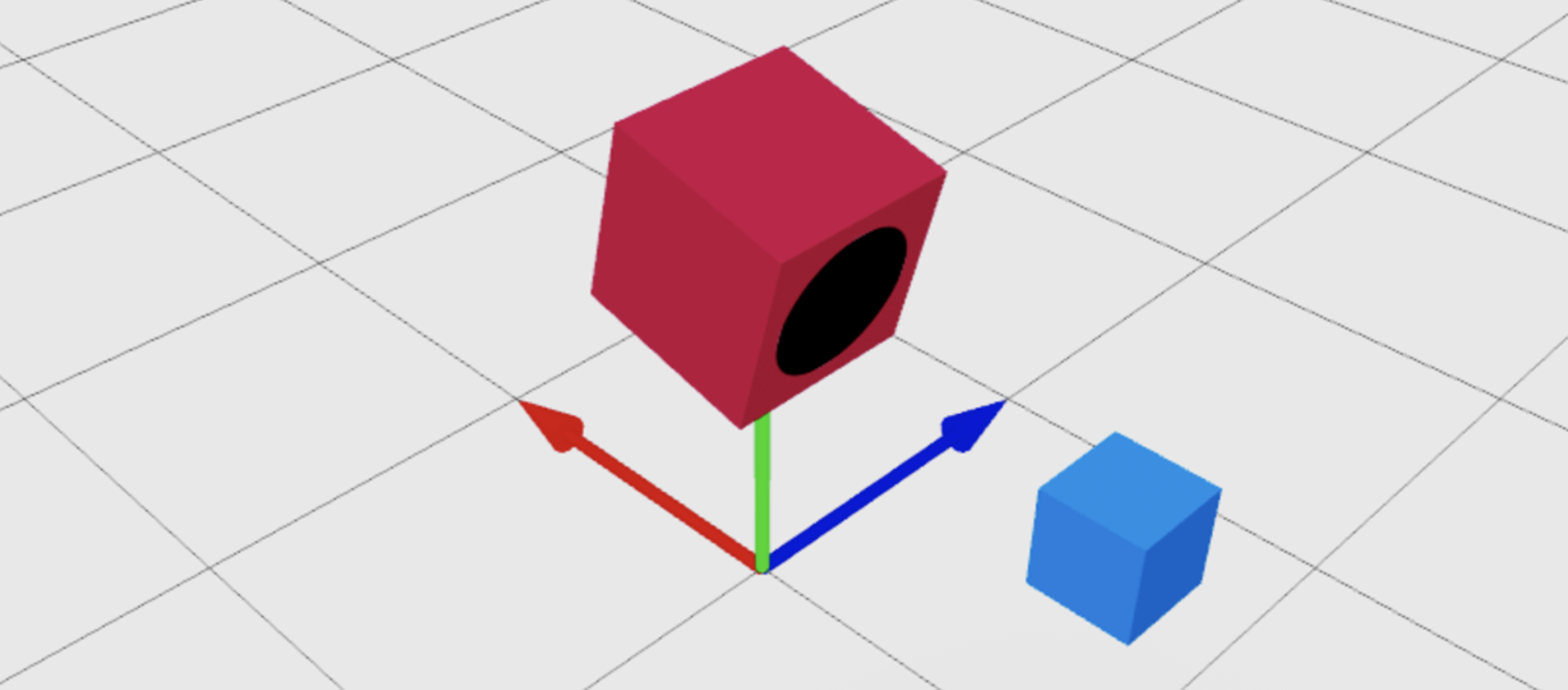
Facing a Specific Surface Toward a Point
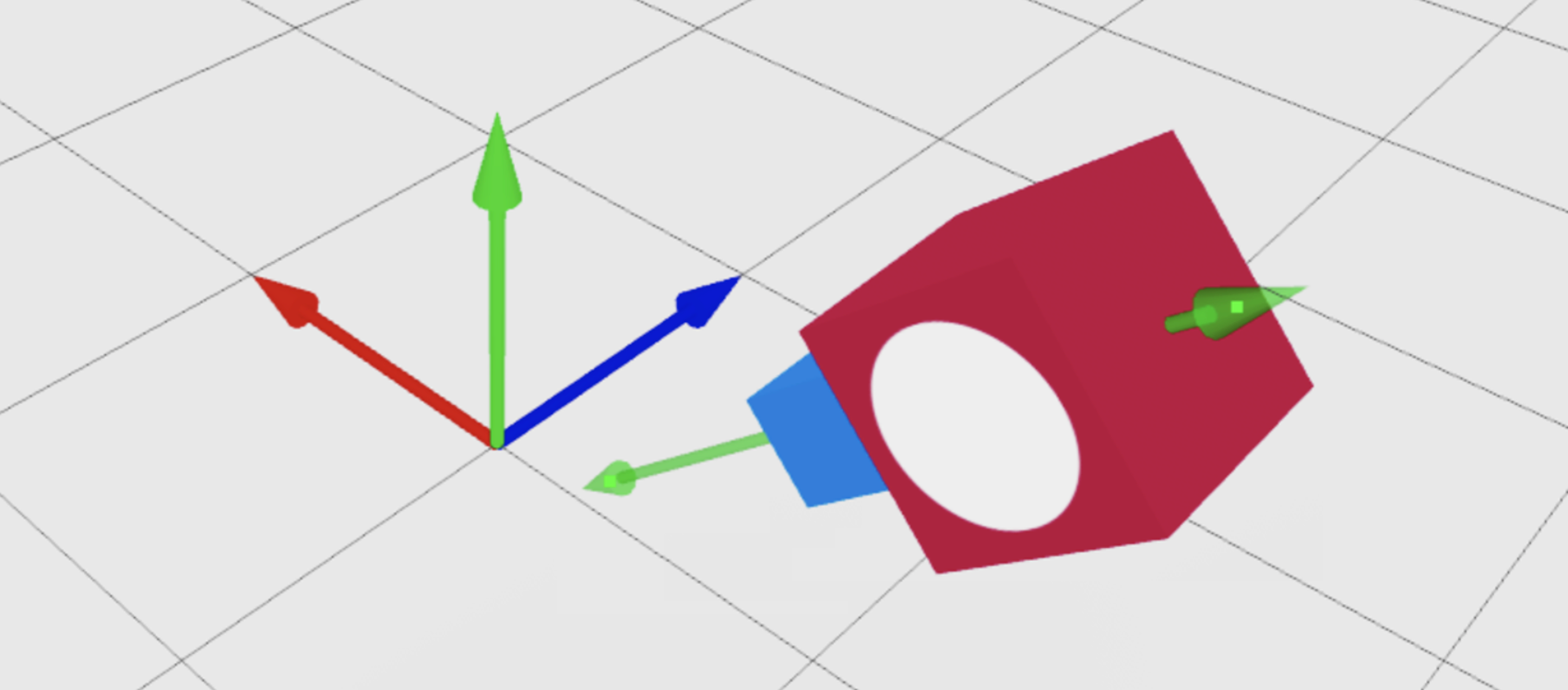
You can make the front of an object face another object by supplying a Vector3 point as the second parameter of CFrame.new(). You can also use relative rotation to make any face of the object point toward a Vector3 point. The following example performs two consecutive CFrame operations:
- Point the front surface, marked by the white circle, at the target.
- Rotate the CFrame to make the top surface, marked by the black circle, point toward the target.
Finding a Point Between Points
You can use linear interpolation, or lerp, to position a CFrame between two points. In the following example, the redBlock part repositions between the greenCube and cyanCube parts. The value of 0.7 places it 70% of the distance away from the green cube.